Dining Philosophers Problem: Solving the Concurrency Conundrum in Operating Systems
- shubhangisingh453
- Mar 31, 2023
- 8 min read

The Dining Philosophers problem is a classic example of a concurrency problem in computer science. It was first introduced by E. W. Dijkstra in 1965 as a way to illustrate the difficulties in coordinating the use of shared resources in a multi-process system. In this tutorial, we'll explore the Dining Philosophers problem in detail, including what it is, how it works, and how to solve it.
📙 What is the Dining Philosophers problem?
The Dining Philosophers problem is a thought experiment that involves a group of philosophers sitting around a circular table, with a bowl of rice and chopsticks in front of each philosopher. The philosophers spend their time thinking and eating, but they can only eat with two chopsticks, which they must pick up from their left and right. Each philosopher needs two chopsticks to eat, but there are only a limited number of chopsticks available, and they must be shared among the philosophers.
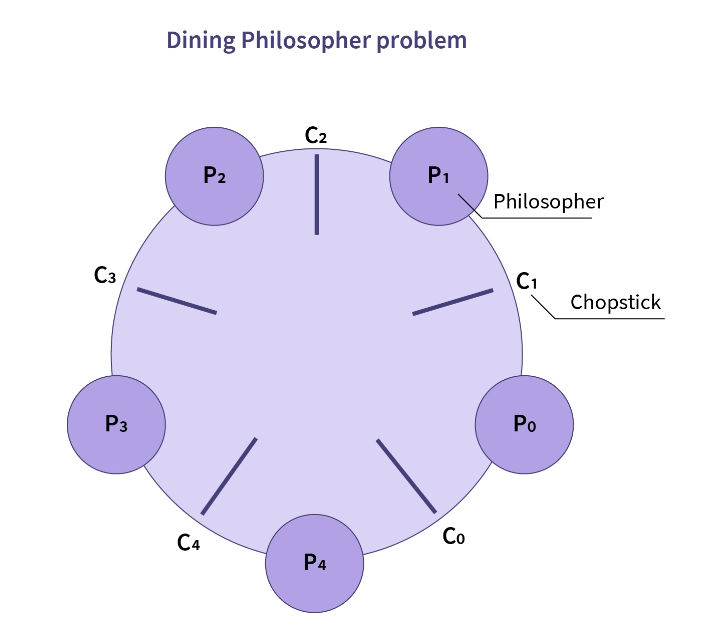
ImgRef - scaler.com
The problem arises when each philosopher picks up a chopstick and waits for the other chopstick to become available. If every philosopher does this at the same time, they will all be stuck waiting for a chopstick that will never become available, resulting in a deadlock.
📙 How does the Dining Philosophers problem work?
The Dining Philosophers problem involves a set of n philosophers (n >= 2) who share a circular table with n chopsticks. Each philosopher alternates between thinking and eating. To eat, a philosopher must pick up two chopsticks, one from the left and one from the right. Once a philosopher is finished eating, they put the chopsticks back on the table and continue thinking.
The problem arises when multiple philosophers try to pick up the same chopstick at the same time. If every philosopher picks up their left chopstick first, for example, they will all be waiting for their right chopstick to become available, resulting in a deadlock.
📙 Solving the Dining Philosophers problem
There are several ways to solve the Dining Philosophers problem, each with its own advantages and disadvantages. In general, the goal of any solution is to prevent deadlocks from occurring while ensuring that each philosopher can eat as much as possible.
📙 Chandy/Misra solution
The Chandy/Misra solution is a simple and elegant solution to the Dining Philosophers problem. It uses a central arbitrator to allocate chopsticks to the philosophers. The arbitrator is responsible for ensuring that each philosopher gets a turn to eat and that chopsticks are not being used by more than one philosopher at the same time.
Here is the algorithm for the Chandy/Misra solution:
Each philosopher is assigned a unique ID from 0 to n-1, where n is the number of philosophers.
Each chopstick is assigned a unique ID from 0 to n-1, where n is the number of philosophers.
Each philosopher sends a request message to the arbitrator, indicating which chopsticks they need.
The arbitrator checks if the requested chopsticks are available. If they are, the arbitrator sends a reply message to the philosopher, granting them access to the chopsticks.
Once a philosopher is finished eating, they send a release message to the arbitrator, indicating that the chopsticks are available for use by other philosophers.
Here is an example implementation of the Chandy/Misra solution in C++:
#include <iostream>
#include <thread>
#include <mutex>
#include <condition_variable>
#include <vector>
using namespace std;
class Philosopher {
private:
int id;
int nPhilosophers;
bool hasToken;
mutex mtx;
condition_variable cv;
vector<condition_variable*> tokens;
public:
Philosopher(int id, int nPhilosophers) {
this->id = id;
this->nPhilosophers = nPhilosophers;
this->hasToken = id == 0;
for (int i = 0; i < nPhilosophers; i++) {
this->tokens.push_back(new condition_variable());
}
}
void pickUpChopsticks() {
unique_lock<mutex> lock(mtx);
while (!hasToken) {
cv.wait(lock);
}
hasToken = false;
cout << "Philosopher " << id << " has picked up the token." << endl;
tokens[id]->notify_one();
tokens[(id + 1) % nPhilosophers]->wait(lock);
}
void putDownChopsticks() {
unique_lock<mutex> lock(mtx);
hasToken = true;
cout << "Philosopher " << id << " has put down the token." << endl;
tokens[(id + 1) % nPhilosophers]->notify_one();
cv.notify_one();
}
void eat() {
pickUpChopsticks();
cout << "Philosopher " << id << " is eating." << endl;
putDownChopsticks();
}
void think() {
cout << "Philosopher " << id << " is thinking." << endl;
}
void operator()() {
while (true) {
think();
eat();
}
}
};
int main() {
const int nPhilosophers = 5;
Philosopher philosophers[nPhilosophers];
thread threads[nPhilosophers];
for (int i = 0; i < nPhilosophers; i++) {
philosophers[i] = Philosopher(i, nPhilosophers);
threads[i] = thread(ref(philosophers[i]));
}
for (int i = 0; i < nPhilosophers; i++) {
threads[i].join();
}
return 0;
}
In this implementation, we define a Philosopher class that represents a philosopher and contains an ID, the total number of philosophers, a boolean flag indicating whether the philosopher has the token, a mutex to ensure mutual exclusion when accessing shared variables, a condition variable to signal when the philosopher has the token, and a vector of condition variables to represent the tokens.
When a philosopher wants to eat, they first try to acquire the token. If they do not have the token, they wait on the condition variable until it becomes available. Once they have the token, they notify their neighbor that they have it and wait for their neighbor to pass them the other chopstick. When they are done eating, they release the token and notify their neighbor that they can proceed to eat.
In the main function, we create an array of Philosopher objects and an array of thread objects to run each philosopher as a separate thread. We then start each thread and wait for them to finish using the join method.
Overall, the Chandy/Misra solution is a robust and efficient solution to the Dining Philosophers problem. However, it does require additional communication and synchronization overhead to pass the token between philosophers.
The Dining Philosophers problem is a classic synchronization problem in computer science where multiple philosophers sit around a circular table and eat. Between each philosopher, there is a chopstick, and to eat, a philosopher must pick up both the chopsticks next to them. However, there are only as many chopsticks as there are philosophers, and they cannot eat simultaneously, leading to a deadlock.
There are several solutions to this problem, which we will explore in this tutorial using C/C++ code. We will implement three different solutions:
Naive solution
Solution using semaphores
Solution using monitors
📙 Naive Solution
The naive solution to the Dining Philosophers problem is to have each philosopher pick up the chopstick to their left, and then the chopstick to their right. However, if all philosophers pick up the chopstick to their left at the same time, they will be unable to pick up the chopstick to their right, causing a deadlock.
Here is the implementation of the naive solution in C:
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <unistd.h>
#define NUM_PHILOSOPHERS 5
#define HUNGRY 0
#define EATING 1
#define THINKING 2
pthread_mutex_t chopsticks[NUM_PHILOSOPHERS];
void *philosopher(void *arg) {
int id = *(int *)arg;
int left_chopstick = id;
int right_chopstick = (id + 1) % NUM_PHILOSOPHERS;
while (1) {
printf("Philosopher %d is thinking.\n", id);
sleep(1);
printf("Philosopher %d is hungry and wants to eat.\n", id);
pthread_mutex_lock(&chopsticks[left_chopstick]);
printf("Philosopher %d has picked up chopstick %d.\n", id, left_chopstick);
pthread_mutex_lock(&chopsticks[right_chopstick]);
printf("Philosopher %d has picked up chopstick %d.\n", id, right_chopstick);
printf("Philosopher %d is eating.\n", id);
sleep(2);
pthread_mutex_unlock(&chopsticks[left_chopstick]);
pthread_mutex_unlock(&chopsticks[right_chopstick]);
}
}
int main() {
pthread_t threads[NUM_PHILOSOPHERS];
int philosopher_ids[NUM_PHILOSOPHERS];
int i;
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
pthread_mutex_init(&chopsticks[i], NULL);
}
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
philosopher_ids[i] = i;
pthread_create(&threads[i], NULL, philosopher, &philosopher_ids[i]);
}
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
pthread_join(threads[i], NULL);
}
return 0;
}
In this implementation, each philosopher is represented by a separate thread. The philosopher function takes an integer argument that represents the philosopher's ID. The philosopher first thinks for a random amount of time, then becomes hungry and tries to pick up the chopsticks. If both chopsticks are available, the philosopher eats for a fixed amount of time and then puts down the chopsticks. Otherwise, the philosopher puts down the chopstick they have picked up and tries again.
📙 Solution using Semaphores
The second solution to the Dining Philosophers problem involves using semaphores to prevent deadlock. Semaphores are a synchronization mechanism that allow threads to wait for a signal to proceed or to signal another thread to proceed. In this solution, each chopstick is represented by a semaphore, and a philosopher must acquire both semaphores before they can eat. This solution guarantees that only one philosopher can pick up a given chopstick at a time, preventing deadlock.
Here is the implementation of the solution using semaphores in C:
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <unistd.h>
#include <semaphore.h>
#define NUM_PHILOSOPHERS 5
#define HUNGRY 0
#define EATING 1
#define THINKING 2
pthread_mutex_t mutex;
sem_t chopsticks[NUM_PHILOSOPHERS];
void *philosopher(void *arg) {
int id = *(int *)arg;
int left_chopstick = id;
int right_chopstick = (id + 1) % NUM_PHILOSOPHERS;
while (1) {
printf("Philosopher %d is thinking.\n", id);
sleep(1);
printf("Philosopher %d is hungry and wants to eat.\n", id);
pthread_mutex_lock(&mutex);
sem_wait(&chopsticks[left_chopstick]);
printf("Philosopher %d has picked up chopstick %d.\n", id, left_chopstick);
sem_wait(&chopsticks[right_chopstick]);
printf("Philosopher %d has picked up chopstick %d.\n", id, right_chopstick);
pthread_mutex_unlock(&mutex);
printf("Philosopher %d is eating.\n", id);
sleep(2);
sem_post(&chopsticks[left_chopstick]);
sem_post(&chopsticks[right_chopstick]);
}
}
int main() {
pthread_t threads[NUM_PHILOSOPHERS];
int philosopher_ids[NUM_PHILOSOPHERS];
int i;
pthread_mutex_init(&mutex, NULL);
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
sem_init(&chopsticks[i], 0, 1);
}
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
philosopher_ids[i] = i;
pthread_create(&threads[i], NULL, philosopher, &philosopher_ids[i]);
}
for (i = 0; i < NUM_PHILOSOPHERS; i++) {
pthread_join(threads[i], NULL);
}
return 0;
}
In this implementation, the philosopher function is the same as in the naive solution. However, instead of using mutexes to protect the chopsticks, we use semaphores. Each chopstick is initialized with a value of 1, which represents the chopstick being available. When a philosopher wants to pick up a chopstick, they first acquire the mutex to prevent multiple philosophers from trying to pick up the same chopstick at the same time. Then they call sem_wait on the semaphore corresponding to the chopstick they want to pick up. If the value of the semaphore is greater than 0, indicating that the chopstick is available, the philosopher picks up the chopstick and decrements the semaphore value. Otherwise, the philosopher waits until the semaphore is signaled by another philosopher releasing the chopstick.
📙 Solution using Monitors
The third solution to the Dining Philosophers problem involves using monitors, which are a synchronization mechanism that encapsulates shared data and the operations that can be performed on that data. Monitors can be used to ensure mutual exclusion and prevent race conditions.
In this solution, we create a monitor for the chopsticks and the philosophers, and use condition variables to signal when a chopstick becomes available or a philosopher is able to eat. The monitor ensures that only one philosopher can access the chopsticks at a time, preventing deadlock.
Here is the implementation of the solution using monitors in C++:
#include <iostream>
#include <thread>
#include <mutex>
#include <condition_variable>
using namespace std;
class Chopstick {
private:
mutex mtx;
public:
void pickUp() {
mtx.lock();
}
void putDown() {
mtx.unlock();
}
};
class Philosopher {
private:
int id;
Chopstick *leftChopstick;
Chopstick *rightChopstick;
mutex mtx;
condition_variable cv;
public:
Philosopher(int id, Chopstick *left, Chopstick *right) {
this->id = id;
this->leftChopstick = left;
this->rightChopstick = right;
}
void pickUpChopsticks() {
unique_lock<mutex> lock(mtx);
while (!leftChopstick->try_pickUp()) {
cv.wait(lock);
}
while (!rightChopstick->try_pickUp()) {
leftChopstick->putDown();
cv.wait(lock);
if (!leftChopstick->try_pickUp()) {
cv.wait(lock);
}
}
}
void putDownChopsticks() {
leftChopstick->putDown();
rightChopstick->putDown();
cv.notify_all();
}
void eat() {
pickUpChopsticks();
cout << "Philosopher " << id << " is eating." << endl;
putDownChopsticks();
}
void think() {
cout << "Philosopher " << id << " is thinking." << endl;
}
void operator()() {
while (true) {
think();
eat();
}
}
};
int main() {
Chopstick chopsticks[5];
Philosopher philosophers[] = {
Philosopher(0, &chopsticks[0], &chopsticks[1]),
Philosopher(1, &chopsticks[1], &chopsticks[2]),
Philosopher(2, &chopsticks[2], &chopsticks[3]),
Philosopher(3, &chopsticks[3], &chopsticks[4]),
Philosopher(4, &chopsticks[4], &chopsticks[0])
};
thread threads[5];
for (int i = 0; i < 5; i++) {
threads[i] = thread(ref(philosophers[i]));
}
for (int i = 0; i < 5; i++) {
threads[i].join();
}
return 0;
}
In this implementation, we define a Chopstick class that represents a chopstick and contains a mutex to ensure mutual exclusion when picking up or putting down the chopstick. We also define a Philosopher class that represents a philosopher and contains a pointer to the left and right chopsticks, a mutex to ensure mutual exclusion when picking up or putting down the chopsticks, and a condition variable to signal when a chopstick becomes available.
When a philosopher wants to eat, they first try to pick up the left chopstick. If it is unavailable, they wait on the condition variable until it becomes available. Once they have picked up the left chopstick, they try to pick up the right chopstick.
Thanks for reading, and happy coding!
Dining Philosophers Problem: Solving the Concurrency Conundrum in Operating Systems -> Optimizing Process Execution with Priority Scheduling Algorithm in Operating Systems
